Students encounter and have difficulty with problems that involve direct variation and joint variation. Many of these problems are called
work problems, rate problems, or percent problems. However, many real-life situations involve quantities that change (vary) as a result
of another quantity or quantities. In mathematics, students are introduced to A = l w, s = r
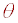 and c = 2
and c = 2 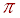 r, as well as the familiar
d = r t and others. In business, they use the revenue formula R = p x and formulas that are based on the common
interest formula I = P r t. In the sciences, students may use formulas like, F = m a, W = F d, w = m g,
PV = T, and many more. I have used a technique that helps students who struggle using these formulas.
r, as well as the familiar
d = r t and others. In business, they use the revenue formula R = p x and formulas that are based on the common
interest formula I = P r t. In the sciences, students may use formulas like, F = m a, W = F d, w = m g,
PV = T, and many more. I have used a technique that helps students who struggle using these formulas.
We consider d = r t as an example. When students are presented with this direct-variation equation, they see that d is the product
of r and t. However, when they are required to find either r or t, they often make an unconscious choice and multiply the two given
values to find the unknown quantity. These students do not recognize that they must divide (not multiply) to find the unknow, and they
often do not know which value divides into the other value. For many students, the problem is that they do not see what to do with the
given values. Although we can solve any given direct-variation equation algebraically for each of the variables involved,
some students then experience additional frustration and confusion because they perceive that they are forced to memorize too many formulas.
To help avoid such frustrationa and confusion, I demonstrate a technique to my students that was shown to me by my chemistry professor, Allen
Hammer,when I was an undergraduate student at West Virginia Wesleyan College. I call it the triangle technique. This technique is
not a substitute for understanding. It is a helpful tool that allows struggling students to get beyond their frustration.
The first step in using the triangle technique is to make sure that the equation (formula) is in the form of a direct variation; that is, the
equation must include one quantity that is isolated and set equal to the product of the other quantities. This step is not a concern
most of the time, since students are introduced to these kinds of equations in this way and thus remember them. For example, when we
ask a student the distance traveled by a car o the area of a rectangle, the words used iindicate the isolated variable (distance and area in
these situations).
The second step in the triangle technique is to draw an augmented triangle as indicated in the following figure:
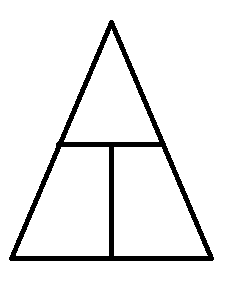
Drawing an isosceles triangle with a horizontal base and a horizontal line segment connecting the midpoints of the legs is helpful.
Students then use a vertical line segment to connect the midpoints of the the horizontal segments.
The third step in the triangle technique is to place each variable from the equation into the appropriate compartment in the triangle.
The isolated variable, usually on the left side of the equation, is placed in the single top compartment. The other two variables
are placed into the compartments at the bottom of the triangle, one in each compartment:
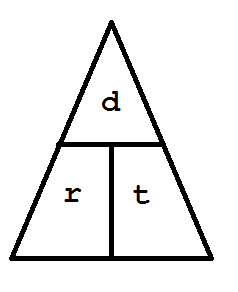
The fourth step in the triangle technique is determing the symbol that represents the unknown in the given problem. Students then
need to solve for that symbol. The student covers that symbol; what remains in the triangle shows where the known values go in the
computation to find the unknown.
We can look at a few examples. How far can a car travel in 7 hours if it is being driven at a constant speed of 55 mph?
Since we are asked how far, we are looking for the distance and cover d to show that it is the unknown. For illustrative
purposes, we replace the unknown with a question mark in the appropriate compartment of the triangle.
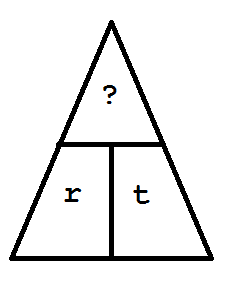
What do we see remaining in the triangle? We see r and t on the same line. Therefore, we must multiply to find the
distance d. The distance traveled would then be 385 miles.
If the question had been, How much time would we need to drive to the beach if we drive at a constant speed of 50 mph and if the
beach is 125 miles away, the triangle would have the following appearance:
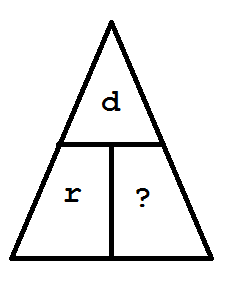
In this problem, we are trying to find time. Then d over r remains in the triangle, so we divide d by r and find the time
to be 2.5 hours.
After students practice using the triangle technique, they have very little trouble modifying it and applying it to more complex
situations. The number of variables on the one side of the equation indicates the number of compartments needed at the bottom
of the triangle. For example, if students need to work a problem involving the basic interest formula I = P r t, they add
a third compartment in the bottom portion of the triangle as follows:
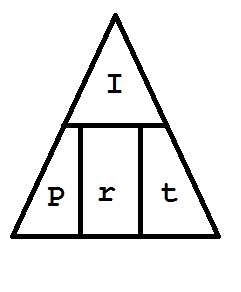
When asked how much time is needed to earn $270 interest on $1500 at an interest rate of 6 percent, students see that they must
divide the interest by both the principal and the rate to find that three years would be needed.
SUMMARY
The triangle is a tool that helps students understand the particular problem; even more important, it helps them become better
at solving direct-variation problems. Students see this tool as a way to solve problems that have always confused and
frustrated them. I always see eyes open wide and expressions of "Ah, now I truly see it." Students still need to
recognize when and how to use the technique. The triangle technique allows students to organize information and helps them
organize the steps required to solve the problem.
 and c = 2
and c = 2 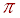 r, as well as the familiar
d = r t and others. In business, they use the revenue formula R = p x and formulas that are based on the common
interest formula I = P r t. In the sciences, students may use formulas like, F = m a, W = F d, w = m g,
PV = T, and many more. I have used a technique that helps students who struggle using these formulas.
r, as well as the familiar
d = r t and others. In business, they use the revenue formula R = p x and formulas that are based on the common
interest formula I = P r t. In the sciences, students may use formulas like, F = m a, W = F d, w = m g,
PV = T, and many more. I have used a technique that helps students who struggle using these formulas.



