Making a connection between mathematics and chemistry (determining the optimal angle between the atoms of covalent bonds) should help answer the trigonometry student's question, "Why do we need to learn these identities and when will we ever use them?" Several trigonometric identities are necessary when doing the proof of the optimal angle for a molecule with four identical atoms bonded to a central atom that has a complete valence shell. This lesson could be taught collaboratively by a chemistry and a mathematics teacher. Manipulatives should be used to aid students' understanding of the lesson.
BASIC INFORMATION
Atoms form covalent bonds with other atoms to create
molecules. A covalent bond is formed when two atoms
share a pair of electrons. The number of covalent bonds
that an atom can form depends on the number of
available electrons found in its outermost (valence)
shell. In a single covalent bond, the sharing of a pair of
electrons forms the bond that holds two atoms together.
However, when considering a polyatomic molecule
(a molecule in which there are two or more atoms
bonded to a central atom) it is important to realize that
there are interactions that occur between the covalent
bonds that determine the three-dimensional shape of
the molecule.
What are these interactions that occur between
covalent bonds? An electron is by definition a negatively
charged atomic particle. In a polyatomic molecule,
there are two or more covalent bonds. Because each
bond is composed of negatively charged electrons. the
negative charges found on the electrons that compose
the bonds repel each other. Ultimately, the molecule
will be arranged in three dimensions such that the
repulsion between the electron pairs of different bonds
is at a minimum. The repulsive forces between the
electron pairs of different covalent bonds causes the
bonds to remain as far apart as possible. The
valence-shell electron-pair repulsion (VSEPR) model is
used by scientists to account for the geometric arrangements of
covalent bonds around a central atom that minimize the
repulsion between the electron pairs of the covalent
bonds.
The simplest molecular shape that can be explained
by the VSEPR model is that of a molecule in which two
atoms are bonded covalently to a central atom to complete
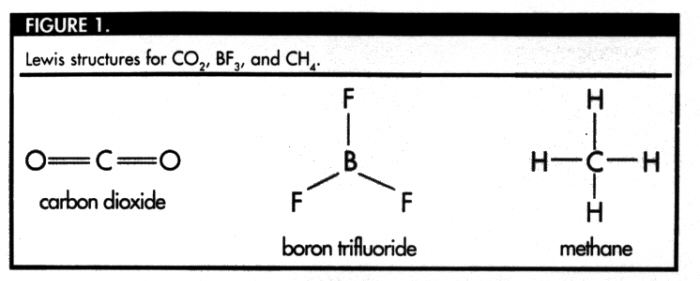
its valence shell. Carbon dioxide (with the molecular formula
CO2)
is an example of a molecule in which two atoms are bonded
covalently to the central atom (C), leaving no nonbonding
pairs of electrons.
A Lewis structure is a two-dimensional
representation of a molecule's structure. The Lewis structure
for CO2 appears in Figure 1. The electron pairs that
create the covalent bonds between the carbon atom and the oxygen
atoms repel each other. In order to minimize the repulsion
between the covalent bonds, the bonds must be separated from
each other by 180°. In this case, the Lewis structure
accurately describes both the two-dimensional and three-dimensional
shape of the molecule. A polyatomic molecule that is composed of
two atoms covalently bonded to a central atom (leaving no
non-bonding pairs of electrons) takes on a linear conformation
and a characteristic bond angle of 180°.
Using the VSEPR model, students can examine the geometry of a
molecule that is composed of three identical atoms covalently
bonded to a central atom, leaving no nonbonding electrons.
Boron trifluoride (BF3 ) is a molecule that fits this
description. The Lewis structure of BF3 that appears
in Figure 1 accounts for molecular shape in only two dimensions.
In reality, the molecule exists in three dimensions. The
two-dimensional molecular model in this figure suggests that the
optimal bond angle for BF3 is 120°, and that all
four atoms of the molecule are in the same plane.
Is there a
three-dimensional conformation that would result in a greater bond
angle and thus a greater distance between the bonds? Intuitively,
the answer is no. If boron were moved out of the plane, the angle
in question (FBF) would become smaller, less than 120°. When this
angle is reduced, the distance between the two fluorine atoms
of the angle is reduced as well.
If the two fluorine atoms move closer to each other, the
electrons that form the bonds are also brought closer
together. If these electrons are brought closer together,
they will experience more repulsion. The three-dimensional
conformation that BF3 must take on in order to
minimize the repulsion between the covalent bonds is
a trigonal planar conformation with an optimal bond
angle of 120°.
A more interesting problem of molecular geometry is
encountered when dealing with a molecule comprised
of four atoms covalently bonded to a central atom leaving no
nonbonding electron pairs. A common example of such a molecule
is methane (CH4). The Lewis structure for
CH4 also appears in Figure 1. The Lewis structure
suggests that the optimal bond angle for methane is 90°.
Does a three-dimensional conformation exist for methane that
would allow bond angles greater than 90°? If such a
conformation exists, the hydrogen atoms would be farther apart
from each other. How does one go about finding the optimal bond
angle that places these four hydrogen atoms at points in
space that are the greatest distance from each other?
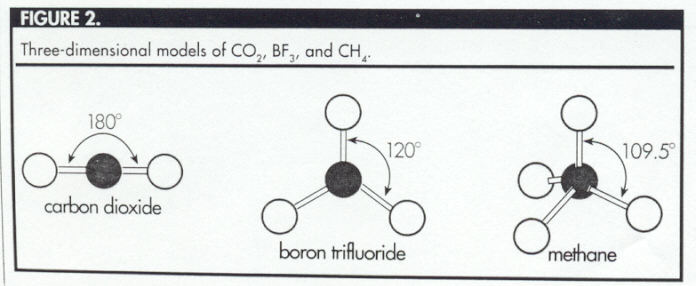
Students should be encouraged to experiment with
manipulatives, such as gum drops and toothpicks or
straws and marshmallows, to build the three-dimensional
models of carbon dioxide, boron trifluoride, and
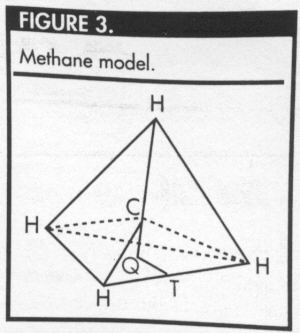
methane (Figure 2). The three-dimensional model of
methane is a tetrahedron, with the carbon atom at the
center of the tetrahedron and the four hydrogen atoms
at the vertices (Figure 3). Students should be encouraged
to construct cardboard or paper triangles for Figures 4, 5,
and 6 and to use a protractor to measure the
bond angles of each of their models. This will help
students to visualize the methane model and understand
the following discussion.
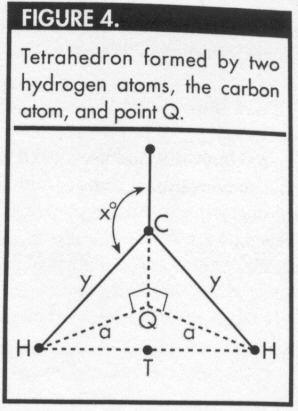
To determine the optimal bond angle, draw a
perpendicular line from the carbon atom (C) to the plane
containing three of the hydrogen atoms. Let Q represent
the foot of this perpendicular line (Figures 3 and 4), and
let y represent the distance between the carbon atom and
any of the hydrogen atoms. Let a represent the distance
from Q to one of the hydrogen atoms, and let x represent
the measure of the required bond angle.
In Figure 3, note that Q is the circumcenter of the
equilateral triangle formed by the three hydrogen atoms
that lie in the bottom plane. Because the triangle HHH is
equilateral, each of the angles HQH measures 120°. In
Figure 4, the measure of angle HCQ = (180-x)° and the measure
of angle CHQ = (x-90)°. It follows that
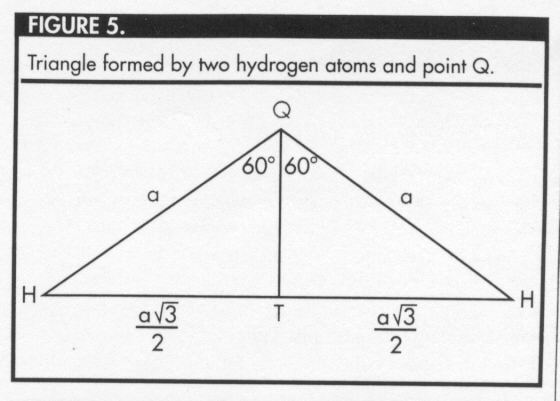
Now, examine the triangle formed by two hydrogen atoms and point Q (Figure 5).
The altitude from point Q divides the triangle HQH into two congruent triangles
HQT and HQT (hypotenuse - leg theorem). So, the vertex angle HQH is divided into
two angles whose measures are each 60°.
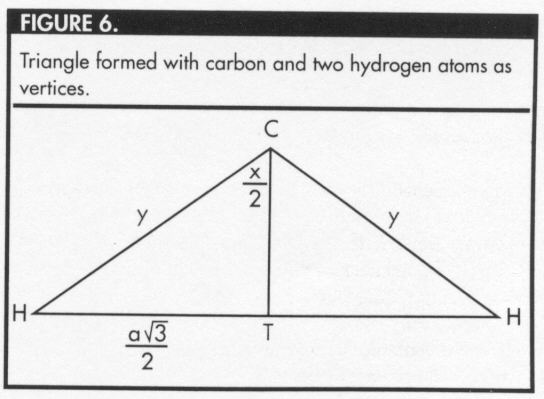
Figure 6 represents the triangle formed by the carbon atom and two hydrogen atoms.
Using the definition of sine, it can be shown that
Using the identity
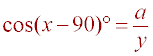 or a = y cos(x- 90)°. Using the
trigonometric identities
or a = y cos(x- 90)°. Using the
trigonometric identities
cos(-A) = cos(A) and cos(90-A)° = sin(A), it follows
that a = y cos(90 -x)° and that a = y sin(x).
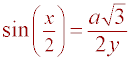 ,
where x is the required bond angle. Now substituting the
half angle identity,
,
where x is the required bond angle. Now substituting the
half angle identity, 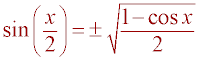 and the
result from above, a = y sin(x), the following equation is obtained:
and the
result from above, a = y sin(x), the following equation is obtained:
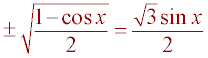 .
.
Squaring both
sides, one obtains the following result: 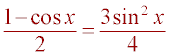 .
.
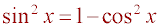 ,
it can be shown that 3cos2(x) - 2cos(x) - 1 = 0 from which cos(x) = -.33 or
cos(x) = 1. Finally, the value of x is 109.5°, which is the measure of the
required bond angle.
,
it can be shown that 3cos2(x) - 2cos(x) - 1 = 0 from which cos(x) = -.33 or
cos(x) = 1. Finally, the value of x is 109.5°, which is the measure of the
required bond angle.
It is important for students to make connections between
mathematics and other disciplines. Knowledge of mathematics
means much more than just memorizing information or facts;
it requires the ability to use information
to reason, think, and solve problems. By themselves,
trigonometric identities are just facts, but applying them
to a real-world problem will give students a deeper
appreciation of those identities and of mathematics.
This manipulation of several trigonometric identities
allows students to discover for themselves
that the optimal bond angle for methane is
109.5°, not 90° as suggested by the 2-dimensional
representation. Hopefully, students will
begin to value and use the connections between mathematics
and other disciplines.
This article was published in the February 1998 issue of The
Science Teacher. At the time, Dr. Pleacher was a medical student
at the Medical College of Virginia, Richmond, Virginia.
Click here for a pdf file of this article