Students learn most effectively if they are able to apply inquiry
and problem-solving skills to problems that emphasize practical
applications. Many experts stress connecting science to other
disciplines, such as mathematics, and modeling word problems to
real-world situations.
Making a connection between mathematics and chemistry (determining
the optimal angle between the atoms of covalent bonds) should help
answer the trigonometry student's question, "Why do we need to
learn these identities and when will we ever use them?" Several
trigonometric identities are necessary when doing the proof of the
optimal angle for a molecule with four identical atoms bonded to a
central atom that has a complete valence shell.
BASIC INFORMATION
Atoms form covalent bonds with other atoms to create
molecules. A covalent bond is formed when two atoms
share a pair of electrons.
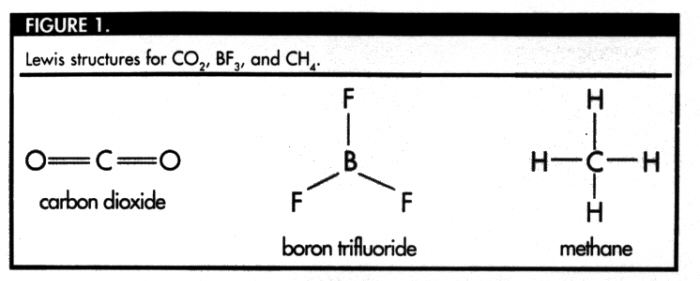
A more interesting problem of molecular geometry is
encountered when dealing with a molecule comprised
of four atoms covalently bonded to a central atom leaving no
nonbonding electron pairs. A common example of such a molecule
is methane (CH4). The Lewis structure for
CH4 also appears in Figure 1. The Lewis structure
suggests that the optimal bond angle for methane is 90°.
Does a three-dimensional conformation exist for methane that
would allow bond angles greater than 90°? If such a
conformation exists, the hydrogen atoms would be farther apart
from each other. How does one go about finding the optimal bond
angle that places these four hydrogen atoms at points in
space that are the greatest distance from each other?
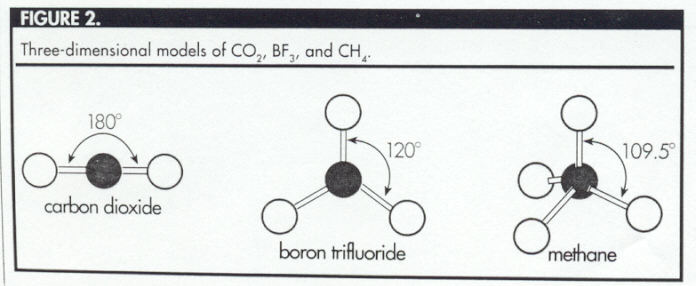
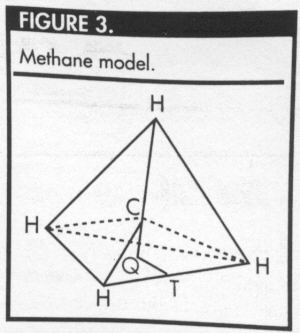
The three-dimensional model of
methane is a tetrahedron, with the carbon atom at the
center of the tetrahedron and the four hydrogen atoms
at the vertices (Figure 3).
To determine the optimal bond angle, draw a
perpendicular line from the carbon atom (C) to the plane
containing three of the hydrogen atoms.
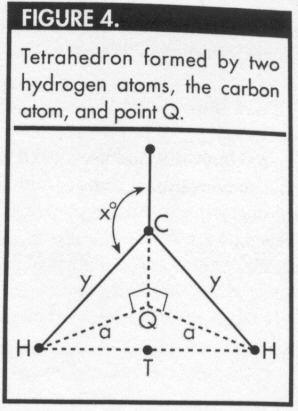
In Figure 3, note that Q is the circumcenter of the
equilateral triangle formed by the three hydrogen atoms
that lie in the bottom plane. Because the triangle HHH is
equilateral, each of the angles HQH measures 120°. In
Figure 4, the measure of angle HCQ = (180-x)° and the measure
of angle CHQ = (x-90)°.
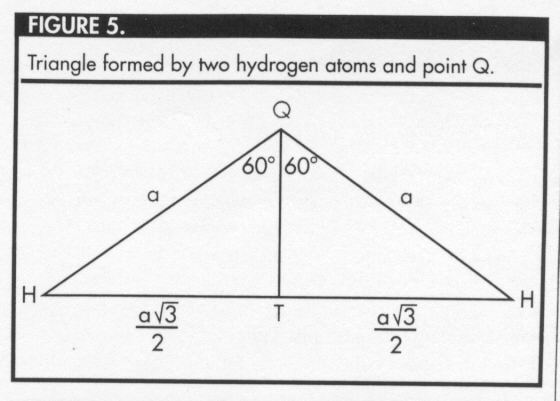
Now, examine the triangle formed by two hydrogen atoms and point Q (Figure 5).
The altitude from point Q divides the triangle HQH into two congruent triangles
HQT and HQT (hypotenuse - leg theorem). So, the vertex angle HQH is divided into
two angles whose measures are each 60°.
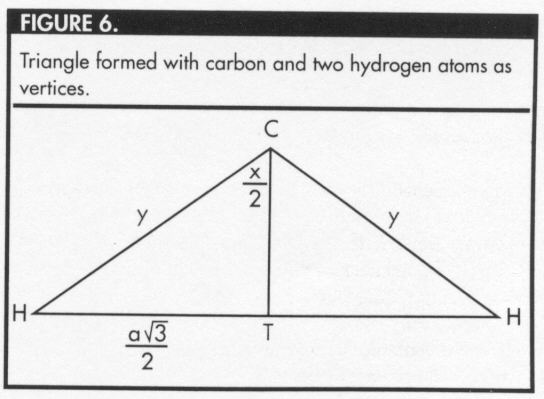
Figure 6 represents the triangle formed by the carbon atom and two hydrogen atoms.
Let Q represent the foot of this perpendicular line (Figures 3 and 4), and
let y represent the distance between the carbon atom and
any of the hydrogen atoms.
Let a represent the distance
from Q to one of the hydrogen atoms, and
let x represent the measure of the required bond angle.
Statements
Reasons
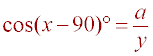
Definition of cosine = adjacent / hypotenuse
a = y cos(x- 90)°
Multiplication Property of Equality
a = y (cos(-(90-x)))
Distributive Property (Factored out -1)
a = y (cos(90 - x))
cos(-A) = cos(A)
a = y sin(x)
cos (90 - A) = sin(A)
Statements
Reasons
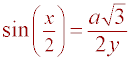
Definition of sine = opposite / hypotenuse
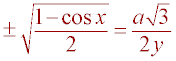
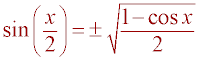
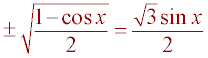
Substitution (Sub a = y sin(x) into previous step)
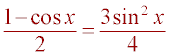
Square both sides
2 - 2cos(x) = 3 (1 - cos2x)
Multiplication Property of Equality
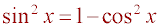
2 - 2cos(x) = 3 - 3 cos2x
Distributive Property
3 cos2x - 2 cos(x) - 1 = 0
Addition Property of Equality
(3 cos(x) + 1) (cos(x) - 1) = 0
Factor (Distributive Property)
cos (x) = -1/3 or cos(x) = 1
Set each factor = 0 (Mult. Prop. of 0)
Muliplication Property of Equality
so x = 109.4712206°
Inverse Cosine
It is important for students to make connections between
mathematics and other disciplines. Knowledge of mathematics
means much more than just memorizing information or facts;
it requires the ability to use information
to reason, think, and solve problems. By themselves,
trigonometric identities are just facts, but applying them
to a real-world problem will give students a deeper
appreciation of those identities and of mathematics.
This manipulation of several trigonometric identities
allows students to discover for themselves
that the optimal bond angle for methane is
109.5°, not 90° as suggested by the 2-dimensional
representation. Hopefully, students will
begin to value and use the connections between mathematics
and other disciplines.
You may read the whole article at:
Covalent bonds and Trigonometry