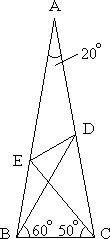
Let ABC be an isosceles triangle (AB = AC) with angle BAC = 20°.
Point D is on side AC such that angle DBC = 60°.
Point E is on side AB such that angle ECB = 50°.
Find the measure of angle EDB.


 

Solution to the Problem:

Angle EDB = 30°.

This geometry problem dates back to at least 1922, when it appeared in the Mathematical Gazette, Volume 11, p. 173. It appears to be an easy problem, but it is deceivingly difficult.

I tried to solve the problem using the following facts:

  • If two sides of an isosceles triangle are congruent,
    Then the angles opposite those sides are congruent.
  • The sum of the measures of the three angles of a triangle is 180°.
  • The sum of the measures of the angles which form a line is 180°.
  • The sum of the measures of the four angles of a quadrilateral is 360°.

After working through the angles in the bottom of the triangle,
I was left with four angles that I couldn't find.
I let x = angle BDE, y = angle DEC, w = angle AED, and z = angle ADE.

Then I wrote several equations and tried to solve them simultaneously:
x + y = 110°
w + y = 130°
x + z = 140°
w + z = 160°
x + y + w + z = 270°, etc.
But I had difficulty finding the unique values for x, y, w, and z;
and yet, I knew that there was only one solution.

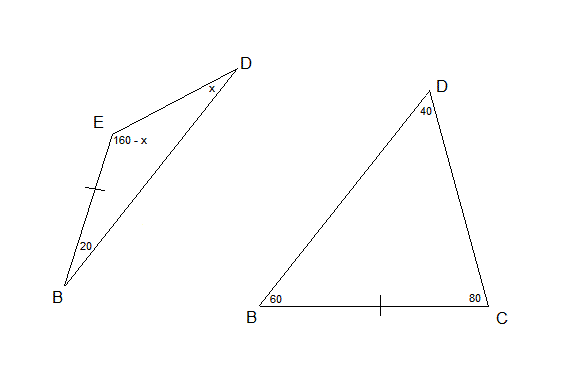
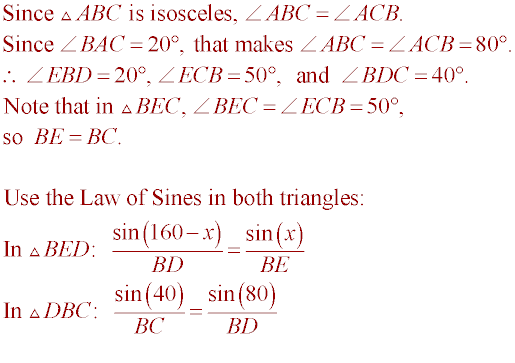
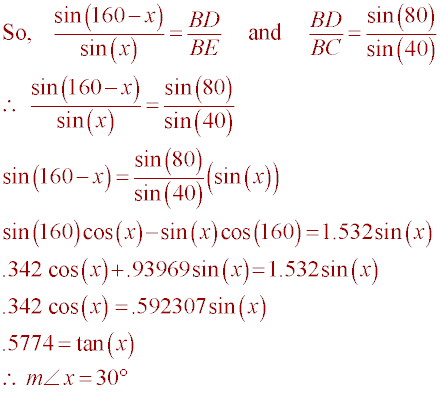
I then tried using trigonometry in the two triangles below (BED and BCD).






Here is the complete solution of the triangle:

    

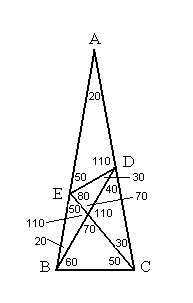
Tom Robb sent in a completely different solution to the problem:

In ABC, let BC=1	<B = < C = 20
in Triangle BEC, <BEC = 50 therefore, BE = BC =1
Draw Altitude AK, and AB = 0.5/cos(80) 
m<ADP=70

With Triangle ADB being isosceles, draw altitude DP 
and BP=1/2(AB) ~1.4396926
PE= BP - BE = 0.4396926
PD = BP*tan(20) ~ 0.52400526

Now <PDE = inverse tangent (PE/PD) = 40

So 70 + 40 + m<EDB + 40 = 180 
and finally, m<EDB = 30 degrees		       





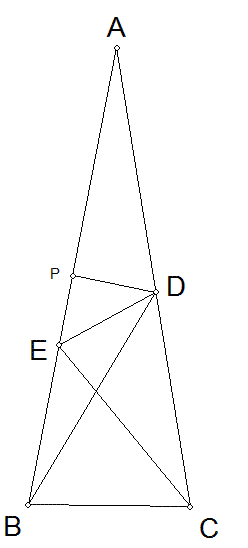
Tristan Collins sent in still a different solution using trig as did Walt Arrison.
Those were the only proofs that were sent, but one of the teachers at my school 
said he did it with just geometry.  Many others drew 
scale drawings to solve the problem.  Below is Walt Arrison's proof:
1) Call the intersection of BD & CE = F
2) Assume the length of AB as 200' (or any distance that you want).
3) Since FBC = 60°, and FCB = 50°, BFC & EFD = 70°. (Note: by subtraction ABD = 20° and ACE = 30°)
4) BFE & CDE = 110°, FBE = 50°, & FDC = 40°.
5) Sin A/2 x 200 = 34.73.
6) BC = 69.46.
7)Sin 70° : 69.46 = Sin 60° : CF = Sin 50° : BF. 
BF = 56.62, CF = 64.015.
8) Sin 110° : BE = Sin 20° : EF = Sin 50° : BF. 
EF = 25.28, BE = 69.46 (Hmmm - another isosceles triangle!)
9) Sin 110° : CD = Sin 30° : DF = Sin 40° : CF.
CD = 93.583, DF = 49.795.
 
10) DE2 = EF2 + DF2 - 2 x EF x DF x cos EFD  
11) DE2 = 25.282 + 49.7952 - (2 x 25.28 x 49.795) x cos 70°
12) DE = 47.513
13) Sin 70° : 47.513 = Sin EDF : 25.28.
14) EDF = 30°.

Correctly solved by:

1. Walt Arrison Philadelphia, Pennsylvania
2. Mike Singer Winchester, Virginia
3. Cameron S. Columbus, Georgia
4. David & Judy Dixon Bennettsville, South Carolina
5. Tom Robb Winchester, Virginia
6. Wajih Ansari Harrisonburg, Virginia
7. Mac Dillon Columbus, Georgia
8. Jeffrey Gaither Winchester, Virginia
9. Arsalan Heydarian Harrisonburg, Virginia
10. Tristan Collins Winchester, Virginia
11. Daniel Gardiner Winchester, Virginia
12. Hamza Rashid Harrisonburg, Virginia
13. Rob Adams Winchester, Virginia
14. Daniel Surber Winchester, Virginia
15. James Alarie University of Michigan -- Flint,
Flint, Michigan
16. Okechi Egekwu Harrisonburg, Virginia