Möbius Strip
One of my favorite math activities is the Möbius Strip. I first saw it demonstrated when I observed a math class taught by Don Buttermore and Don Tomb in 1967 at Gunston Junior High School in Arlington, Virginia. The Möbius Strip or Möbius Band was named after August Ferdinand Möbius, a nineteenth century German mathematician, who was a pioneer in the field of topology.
You take a long strip of paper, twist one of the ends half a turn, and tape the two ends together. The result is a circular hoop with the intriguing property of having only one surface and only one edge. (Incidentally, the three-arrow symbol commonly used to denote "recyclable" is in the form of a Mobius strip.)
Giant Möbius Strips have been used as conveyor belts (to make them last longer, since "each side" gets the same amount of wear) and as continuous-loop recording tapes (to double the playing time). Möbius strips have been used as typewriter ribbons and then as printer ribbons. In the 1960's Sandia Laboratories used Möbius Strips in the design of versatile electronic resistors. Möbius strips have been used in advertising -- a flat triangular möbius strip was used as a symbol of EXPO '74; New Yorker's cover of April 5, 1976 pictured a Möbius Strip around which 30 business people were walking.
And here are some patents based on the Möbius Strip:
Pat. #1,442,632-1923: Lee DeForest: filmstrip -- sound on "both sides";
Pat. #2,479,929-1949: O.H. Harris -- abrasive belt;
Pat. #2,784,834-1957: B.F. Goodrich -- abrasive belt.
Here are some poems about Möbius Strips:
A New Solution to an Old Problem
by Eleanor Ninestein
The Topologist's child was quite hyper
'Til she wore a Moebius diaper.
The mess on the inside
Was thus on the outside
And it was easy for someone to wipe her.
The Mobius Strip
A mathematician confided
That a Mobius band is one-sided.
And you'll get quite a laugh
If you cut it in half,
For it stays in one piece when divided.
The famous artist, M.C. Escher, used the Möbius strip in several of his works of art:

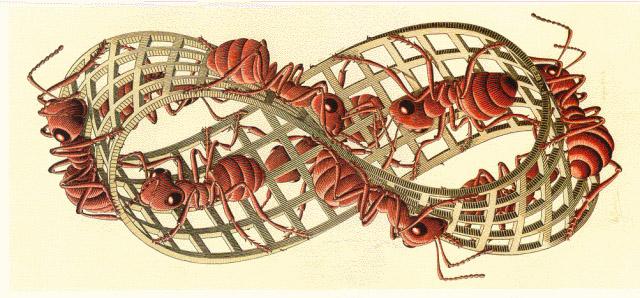

John Hey pointed out that the third picture is not really a Mobius strip. It has two sides (not one).
The silver side is separate from the gold side except where they intersect in the middle, so perhaps you could call it one side!
I have used the Möbius strip in my classroom both as a demonstration and as a hands on activity. I find that
students really enjoy doing this activity on their own. Either way, I use the following activities:
(1) Make a Möbius strip.
(2) Show its one-sidedness by tracing with a pencil or marker
(3) Show it has only one edge by holding the Möbius strip with one hand and tracing along the edge
(4) Cut the Möbius strip down the center
(5) Make another Möbius strip and cut by starting one-third from one of the edges
(6) This last activity is my favorite -- I saw it demonstrated by Fred Pence at a V2CTM Meeting
in Harrisonburg, Virginia. You take two strips (one Möbius and one not) and tape them to each
other at right angles. Then cut them both down the middle.
Click here for detailed instructions and photos of these activities


Below is a video of the Mobius Strip:
No Magic At All: Mobius Strip - video powered by Metacafe