Doug Reiss from Memphis, Tennessee wrote to me that he found the trick in a book by Shakuntala Devi called, Figuring: The Joy of Numbers published in 1977.
So GAMES must have gotten it from there.
From GAMES:
We don't know how this multiplication trick works, but it's
never failed us yet. Take any two
numbers: say, 116 and 3,011.
Halve the first number again
and again, discarding any fractional remainder, until you reach
the number 1. Thus: 116, 58, 29,
14, 7, 3, 1. Double the second as
many times as you halved the
first. Thus: 3,011; 6,022; 12,044;
24,088; 48, 176; 96,352; 192,704.
Write these series alongside
each other, and cross out every
even number in the halves column and its partner in the doubles
column. Thus, as shown in
the following columns, the even
numbers in the halves column
(116, 58, and 14) are crossed out
along with their companions in
the doubles column (3,011;
6,022; and 24,088), regardless of
whether these are even or odd.

Add the numbers that remain in
the doubles column only. The resulting sum will be equal to the
product of the two numbers you
started with.
Thus: 12,044 + 48,176 + 96,352 + 192,704 = 349,276 = 116 X 3,011.
Explanation of the Trick
In February 2015, Shekhar Dutta from the Sarwan Memorial School in West Bengal, India sent me an explanation of the trick. He showed that it can be explained by using base two!
I will give a short summary of his idea and then attach his letter below.
Example 1 -- the problem above: 116 x 3011 = 349,276
The number 116 can be written in terms of powers of two:
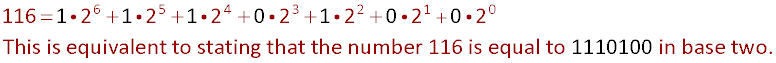
Now use the distributive property:

Example 2 -- 13 x 7 = 91
Here is the trick:

Here is the explanation using the powers of two:
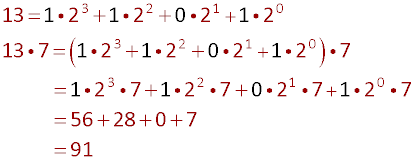
Example 3 -- 15 x 8 = 120
Here is the trick:

Note that there are no even numbers in the first column, so nothing was crossed out.
Here is the explanation using the powers of two:
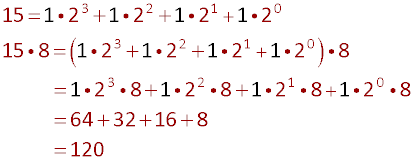
Example 4 -- 8 x 15 = 120
Here is the trick:

Here is the explanation using the powers of two:
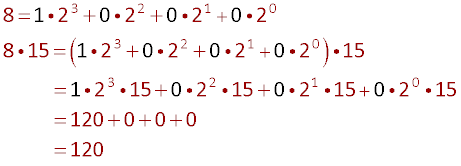
Examples 3 and 4 were the same problem but they look different in the trick;
in example 3, there were no even numbers in the first column; but in example 4, all the
numbers in the first column were even except the last one (which was the answer).
Thanks again to Shekhar for providing the explanation!
Here is Shekhar's letter (some plus signs were omitted):
I am a student from India. I am 15 years old. My English may be a
little poor. I have visited your website 'Mr. P's Math Page'. From
there 'Puzzles and Games', 'Math Trick', 'Number and Computational
Tricks', 'Multiplication Trick'. In this sequence I have reached the
trick of multiplying two numbers.
It said that we have to half one number till it reaches 1, and double
the second number. After canceling the even number(s) in the first
part and the corresponding numbers in the second part, the sum of the
leftover numbers in the second part will be the product of the two
numbers. You said that you don't know an explanation for this trick.
Here I am trying to give an explanation.
(I have not taken any help from anyone to find this explanation. I
would like to get a reply of this mail as soon as possible.)
*You said if the first number is odd after halving we will discard the
fraction. It is like subtracting 1 and dividing by 2.
13/2=6.5, after discarding fraction, =6
Also 13-1=12, 12/2=6
*After subtracting 1 (if necessary) and dividing by 2 as we make 1 we
make a binary representation of the number.
13-1=12, 12/2=6 (1)
6/2=3 (0)
3-1=2, 2/2=1 (1)
1 (1)
Or 13 (1)
6 (0)
3 (1)
1 (1)
Therefore 13(base 2) =1101
This can also be written as 2^3 * 1 + 2^2 * 1 + 2^1 * 0 + 2^0 * 1 = 13
Or 8 + 4 + 1 = 13
Therefore multiplying a number by 13 = Multiplying the number by 8 +
Multiplying the number by 4 + Multiplying the number by 1
13x = 8x + 4x + x
*Canceling the even number(s) in the first part means canceling the
0(s) in the number's binary form.
13 1
6 0
3 1
1 1
this become after canceling
13 1
3 1
1 1
This digits can be represented as
13 1 1
3 1 4
1 1 8
The last column sums to the number taken
*This can be expanded as
13 1 1 x
6 0 0 2x
3 1 4 4x
1 1 8 8x
After canceling the even digits
13 1 1 x
3 1 4 4x
1 1 8 8x
The last column sums to 13x = 13 * x
*As it is seen, by this method the first number is braked as multiples
of 2. The second number is multiplied with this multiples of 2 and
then the products are added.
Examples
15 * 8
15 1 1 8 * 1 = 8
7 1 2 8 * 2 = 16
3 1 4 8 * 4 = 32
1 1 8 8 * 8 = 64
No even numbers to cancel
15 * 8 = 8 + 16 + 32 + 64 = 120
Or 8 * 15
8 0 0 15 * 1 = 15
4 0 0 15 * 2 = 30
2 0 0 15 * 4 = 60
1 1 8 15 * 8 = 120
After canceling the even numbers
1 1 8 15 * 8 = 120
8 * 15 = 120
I hope this explanation will help.
Waiting for reply.

Here is the explanation using the powers of two:
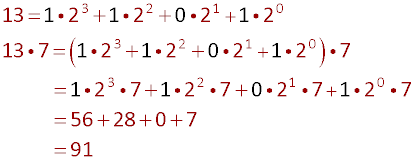
Example 3 -- 15 x 8 = 120
Here is the trick:

Note that there are no even numbers in the first column, so nothing was crossed out.
Here is the explanation using the powers of two:
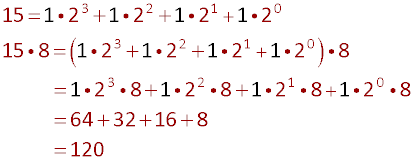
Example 4 -- 8 x 15 = 120
Here is the trick:

Here is the explanation using the powers of two:
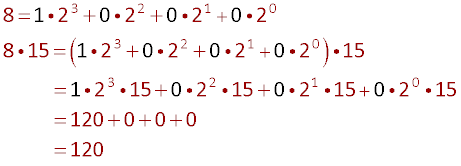
Examples 3 and 4 were the same problem but they look different in the trick;
in example 3, there were no even numbers in the first column; but in example 4, all the
numbers in the first column were even except the last one (which was the answer).
Thanks again to Shekhar for providing the explanation!
Here is Shekhar's letter (some plus signs were omitted):
I am a student from India. I am 15 years old. My English may be a
little poor. I have visited your website 'Mr. P's Math Page'. From
there 'Puzzles and Games', 'Math Trick', 'Number and Computational
Tricks', 'Multiplication Trick'. In this sequence I have reached the
trick of multiplying two numbers.
It said that we have to half one number till it reaches 1, and double
the second number. After canceling the even number(s) in the first
part and the corresponding numbers in the second part, the sum of the
leftover numbers in the second part will be the product of the two
numbers. You said that you don't know an explanation for this trick.
Here I am trying to give an explanation.
(I have not taken any help from anyone to find this explanation. I
would like to get a reply of this mail as soon as possible.)
*You said if the first number is odd after halving we will discard the
fraction. It is like subtracting 1 and dividing by 2.
13/2=6.5, after discarding fraction, =6
Also 13-1=12, 12/2=6
*After subtracting 1 (if necessary) and dividing by 2 as we make 1 we
make a binary representation of the number.
13-1=12, 12/2=6 (1)
6/2=3 (0)
3-1=2, 2/2=1 (1)
1 (1)
Or 13 (1)
6 (0)
3 (1)
1 (1)
Therefore 13(base 2) =1101
This can also be written as 2^3 * 1 + 2^2 * 1 + 2^1 * 0 + 2^0 * 1 = 13
Or 8 + 4 + 1 = 13
Therefore multiplying a number by 13 = Multiplying the number by 8 +
Multiplying the number by 4 + Multiplying the number by 1
13x = 8x + 4x + x
*Canceling the even number(s) in the first part means canceling the
0(s) in the number's binary form.
13 1
6 0
3 1
1 1
this become after canceling
13 1
3 1
1 1
This digits can be represented as
13 1 1
3 1 4
1 1 8
The last column sums to the number taken
*This can be expanded as
13 1 1 x
6 0 0 2x
3 1 4 4x
1 1 8 8x
After canceling the even digits
13 1 1 x
3 1 4 4x
1 1 8 8x
The last column sums to 13x = 13 * x
*As it is seen, by this method the first number is braked as multiples
of 2. The second number is multiplied with this multiples of 2 and
then the products are added.
Examples
15 * 8
15 1 1 8 * 1 = 8
7 1 2 8 * 2 = 16
3 1 4 8 * 4 = 32
1 1 8 8 * 8 = 64
No even numbers to cancel
15 * 8 = 8 + 16 + 32 + 64 = 120
Or 8 * 15
8 0 0 15 * 1 = 15
4 0 0 15 * 2 = 30
2 0 0 15 * 4 = 60
1 1 8 15 * 8 = 120
After canceling the even numbers
1 1 8 15 * 8 = 120
8 * 15 = 120
I hope this explanation will help.
Waiting for reply.

Note that there are no even numbers in the first column, so nothing was crossed out.
Here is the explanation using the powers of two:
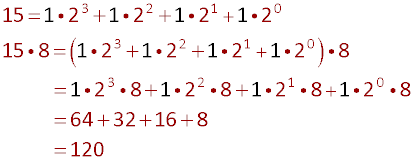
Example 4 -- 8 x 15 = 120
Here is the trick:

Here is the explanation using the powers of two:
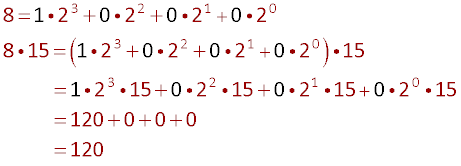
Examples 3 and 4 were the same problem but they look different in the trick;
in example 3, there were no even numbers in the first column; but in example 4, all the
numbers in the first column were even except the last one (which was the answer).
Thanks again to Shekhar for providing the explanation!
Here is Shekhar's letter (some plus signs were omitted):
I am a student from India. I am 15 years old. My English may be a
little poor. I have visited your website 'Mr. P's Math Page'. From
there 'Puzzles and Games', 'Math Trick', 'Number and Computational
Tricks', 'Multiplication Trick'. In this sequence I have reached the
trick of multiplying two numbers.
It said that we have to half one number till it reaches 1, and double
the second number. After canceling the even number(s) in the first
part and the corresponding numbers in the second part, the sum of the
leftover numbers in the second part will be the product of the two
numbers. You said that you don't know an explanation for this trick.
Here I am trying to give an explanation.
(I have not taken any help from anyone to find this explanation. I
would like to get a reply of this mail as soon as possible.)
*You said if the first number is odd after halving we will discard the
fraction. It is like subtracting 1 and dividing by 2.
13/2=6.5, after discarding fraction, =6
Also 13-1=12, 12/2=6
*After subtracting 1 (if necessary) and dividing by 2 as we make 1 we
make a binary representation of the number.
13-1=12, 12/2=6 (1)
6/2=3 (0)
3-1=2, 2/2=1 (1)
1 (1)
Or 13 (1)
6 (0)
3 (1)
1 (1)
Therefore 13(base 2) =1101
This can also be written as 2^3 * 1 + 2^2 * 1 + 2^1 * 0 + 2^0 * 1 = 13
Or 8 + 4 + 1 = 13
Therefore multiplying a number by 13 = Multiplying the number by 8 +
Multiplying the number by 4 + Multiplying the number by 1
13x = 8x + 4x + x
*Canceling the even number(s) in the first part means canceling the
0(s) in the number's binary form.
13 1
6 0
3 1
1 1
this become after canceling
13 1
3 1
1 1
This digits can be represented as
13 1 1
3 1 4
1 1 8
The last column sums to the number taken
*This can be expanded as
13 1 1 x
6 0 0 2x
3 1 4 4x
1 1 8 8x
After canceling the even digits
13 1 1 x
3 1 4 4x
1 1 8 8x
The last column sums to 13x = 13 * x
*As it is seen, by this method the first number is braked as multiples
of 2. The second number is multiplied with this multiples of 2 and
then the products are added.
Examples
15 * 8
15 1 1 8 * 1 = 8
7 1 2 8 * 2 = 16
3 1 4 8 * 4 = 32
1 1 8 8 * 8 = 64
No even numbers to cancel
15 * 8 = 8 + 16 + 32 + 64 = 120
Or 8 * 15
8 0 0 15 * 1 = 15
4 0 0 15 * 2 = 30
2 0 0 15 * 4 = 60
1 1 8 15 * 8 = 120
After canceling the even numbers
1 1 8 15 * 8 = 120
8 * 15 = 120
I hope this explanation will help.
Waiting for reply.

Here is the explanation using the powers of two:
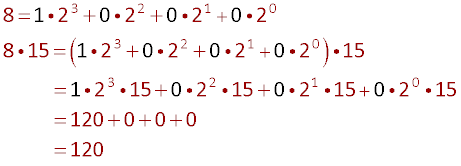
Examples 3 and 4 were the same problem but they look different in the trick;
in example 3, there were no even numbers in the first column; but in example 4, all the
numbers in the first column were even except the last one (which was the answer).
Thanks again to Shekhar for providing the explanation!
Here is Shekhar's letter (some plus signs were omitted):
I am a student from India. I am 15 years old. My English may be a
little poor. I have visited your website 'Mr. P's Math Page'. From
there 'Puzzles and Games', 'Math Trick', 'Number and Computational
Tricks', 'Multiplication Trick'. In this sequence I have reached the
trick of multiplying two numbers.
It said that we have to half one number till it reaches 1, and double
the second number. After canceling the even number(s) in the first
part and the corresponding numbers in the second part, the sum of the
leftover numbers in the second part will be the product of the two
numbers. You said that you don't know an explanation for this trick.
Here I am trying to give an explanation.
(I have not taken any help from anyone to find this explanation. I
would like to get a reply of this mail as soon as possible.)
*You said if the first number is odd after halving we will discard the
fraction. It is like subtracting 1 and dividing by 2.
13/2=6.5, after discarding fraction, =6
Also 13-1=12, 12/2=6
*After subtracting 1 (if necessary) and dividing by 2 as we make 1 we
make a binary representation of the number.