Marios Mamzeris developed this great technique for the construction of odd-order magic squares in 1988 (over thirty years ago) and he has now decided to share it with the public
(all rights reserved). Please visit his website above for his explanation.
To create any odd-order magic square quickly and hassle-free, we just need to make two simple passes, that I describe as table transformations (shifts). The following three
images are depicting the creation of a 31x31 magic square.
1) We first get the full table filled with all numbers from 1 to N2 as we go (1st table image below showing the cells shifting in green color).
Then we make a left shift of all rows, skipping the middle one, starting with moving one number (cell) in the first row while moving an extra more number (cell) in each next row
to N-1 numbers in the last (Nth ) row.
2) The second action is similar to the 1st, but instead of shifting cells in rows, we now shift cells in columns. It starts with moving one number (cell) upwards
from the left side while moving an extra more number (cell) in each next column to N-1 numbers in the last (Nth) column, skipping the middle column this time.
That is the 2nd table image below, showing the cells shifting in blue color).
That's it. A magic square is ready. That is the 3rd image below that also shows the sum of each row, column, and diagonal.
Please visit this short YouTube video which shows all the steps for a 5x5 Magic Square.
You can see the steps for a 7x7 Magic Square here.
1. Initial table with all the numbers from 1 to N2 in sequence (The green arrow shows the direction of the cell shift that will follow and the green cells are the
ones that will shift.)
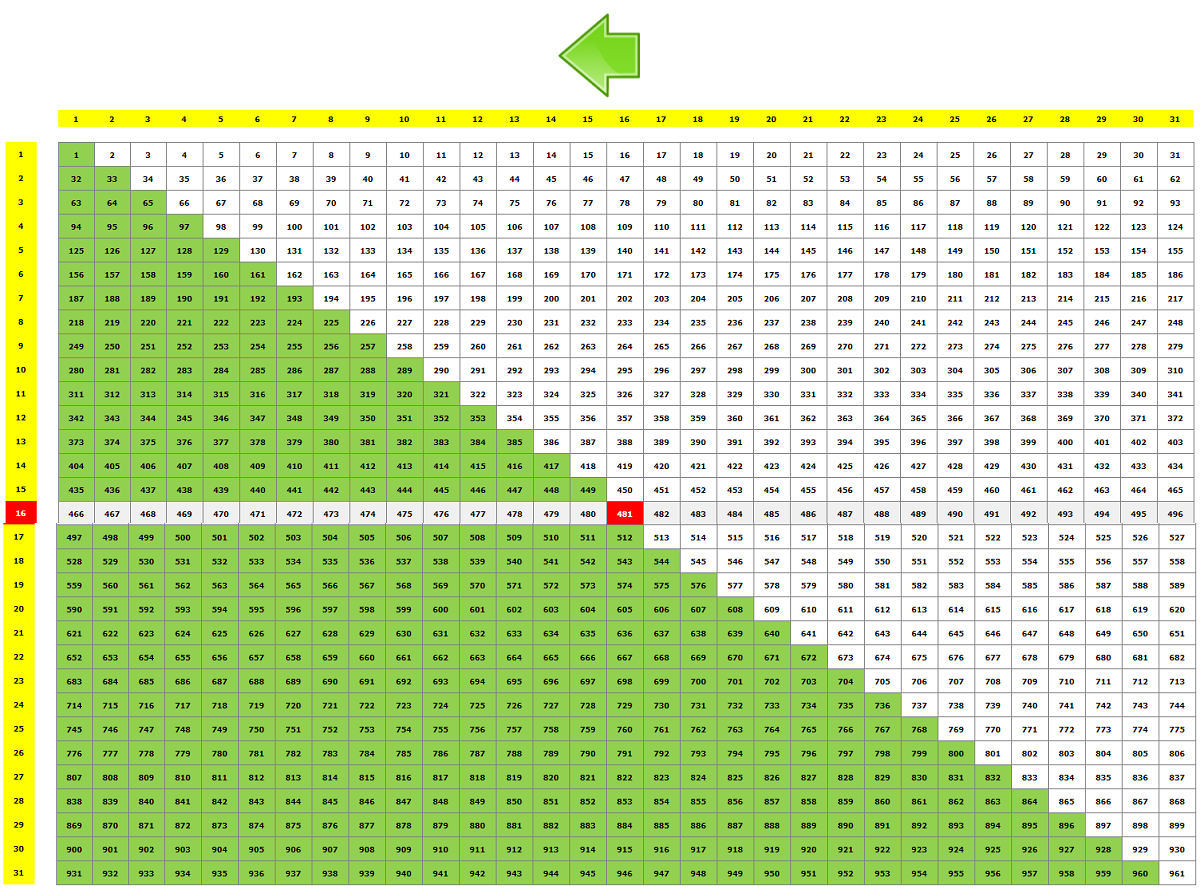
2. First transformation (primary cell shift). This table is the result of the shift depicted in green color above. (The blue arrow shows the direction of the 2nd and
final cell shift and the blue cells are the ones that will shift.)
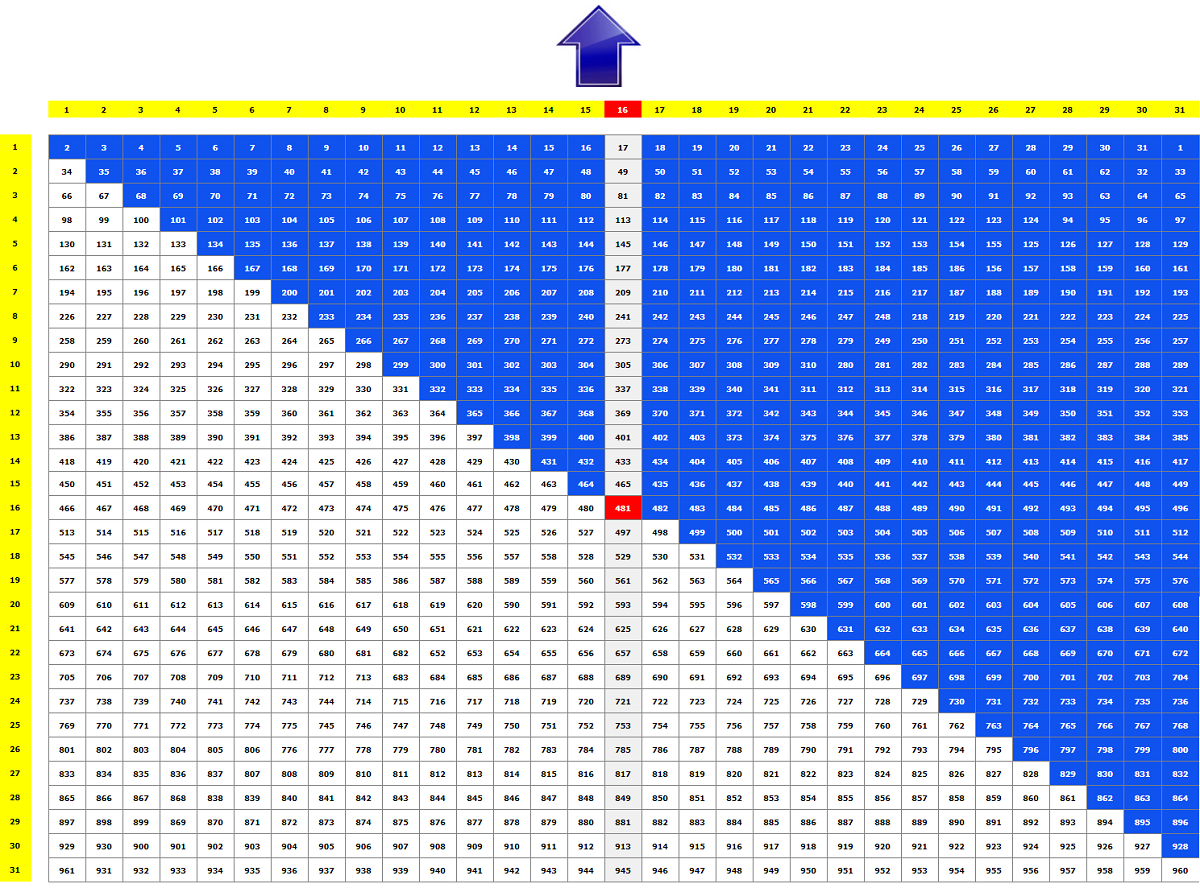
3. Final transformation (secondary cell shift) that gives the Magic Square.

An alternative way (based on the above shift pattern) is to create a magic square by performing the cell shifting in opposite directions for each
half of the table, always skipping the middle row or column.
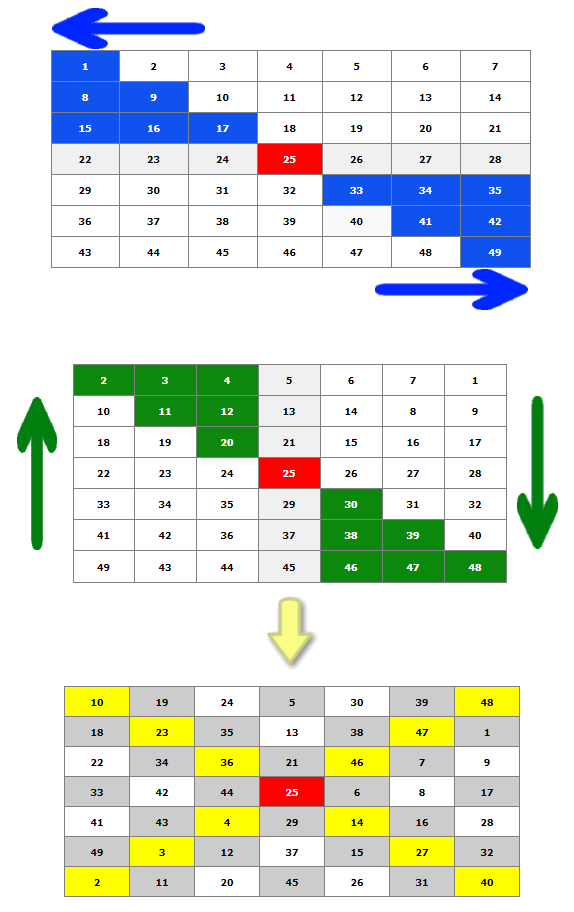
To get different Magic Squares for the same odd order, you may swap the actions. For example, instead of making a Left-shift followed by an Up-shift,
you may try starting with a Right-shift followed by a Down-shift or another combination. Similarly for the alternative way shown above, you may swap
the left-right dual-action per pass with right-left and the down-up with up-down.
Finally, each Magic Square can be turned anticlockwise (or clockwise if you prefer) to produce four (4) different perspectives as shown below.
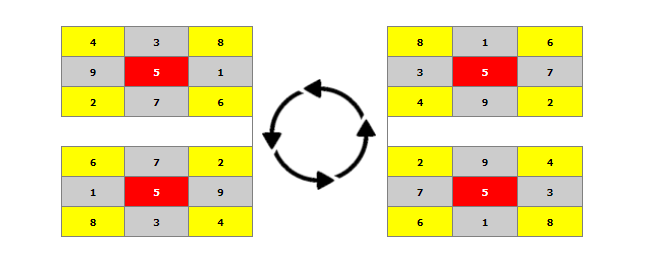
You may get another four (4) versions by mirroring the above magic squares. So, for example, the 3x3 magic square can have eight (8) different solutions.
The mirroring can work for any magic square.




